Binary Search Trees are elegant, but their performance depends entirely on shape. In the worst case, a BST degrades into a linked list, turning logarithmic operations into linear ones.
AVL trees were one of the earliest solutions to this problem, introducing strict self-balancing to guarantee consistent performance.
This article focuses on how AVL trees maintain balance and why that design choice matters, assuming you already know basic BST concepts.
What is an AVL Tree?
An AVL tree is a self-balancing Binary Search Tree where the height difference between the left and right subtrees of every node is tightly controlled.
For each node, a balance factor is defined as:
balance factor = height(left subtree) - height(right subtree)
balance factor ∈ { -1, 0, +1 }
As long as this condition holds, the height of the tree remains O(log n).
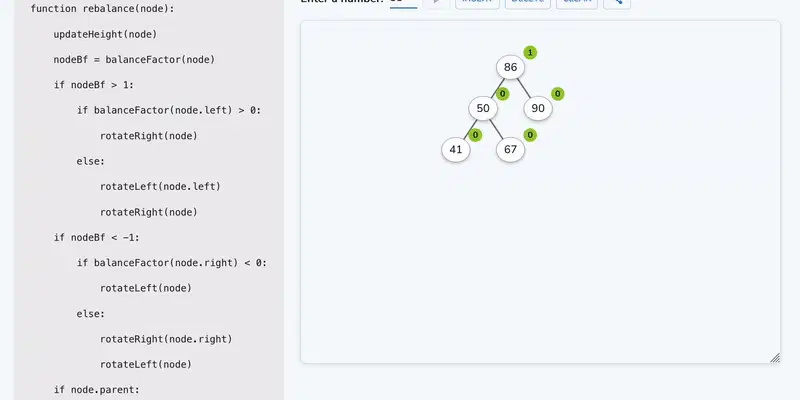
How AVL Tree Restore Balance
AVL trees rely on rotations to restore balance after updates. A rotation is a local restructuring that preserves BST ordering while reducing height imbalance.
There are four canonical imbalance scenarios.
Left-Left (LL) Case
- Insertion occurs in the left subtree of the left child
- Fixed using a single right rotation
Right-Right (RR) Case
- Insertion occurs in the right subtree of the right child
- Fixed using a single left rotation
Left-Right (LR) Case
- Insertion occurs in the right subtree of the left child
- Fixed using:
- Left rotation on the left child
- Right rotation on the unbalanced node
Right-Left (RL) Case
- Insertion occurs in the left subtree of the right child
- Fixed using:
- Right rotation on the right child
- Left rotation on the unbalanced node
Insertion in an AVL Tree
Insertion starts exactly like a normal BST insertion. The difference appears during recursion unwinding:
- Insert the node using BST rules
- Update heights on the path back
- Compute balance factors
- Perform rotations when balance is violated
Only the first unbalanced ancestor needs correction; the rest of the tree automatically stabilizes.
Deletion in an AVL Tree
Deletion is more complex than insertion. Removing a node may reduce subtree height, which can:
- Trigger imbalance
- Propagate imbalance upward
- Require multiple rotations
The overall flow remains:
BST deletion → height update → rebalance
AVL Trees vs Red-Black Trees
A practical comparison:
-
AVL Trees
- Stricter balance
- Faster lookups
- More rotations during updates
-
Red-Black Trees
- Looser balance
- Slightly slower lookups
- Faster inserts and deletes
This tradeoff explains why AVL trees are often used in read-heavy systems, while Red-Black trees dominate standard libraries.
Visualizing AVL Trees
Rotations are easier to understand visually than algebraically. If you prefer step-by-step visual explanations, explore AVL tree animation on:
👉 https://see-algorithms.com/data-structures/AVL
The focus there is on structural change, not just value movement, which closely matches how AVL balancing actually works.
Final Thoughts
AVL trees represent a disciplined and predictable approach to balancing. They are not always the fastest to update, but they excel at guaranteeing performance bounds.
If you understand the invariant, the rotations become a natural consequence—not a memorization exercise.